Surface Regularity via the Estimation of Fractional Brownian Motion Index

Abstract

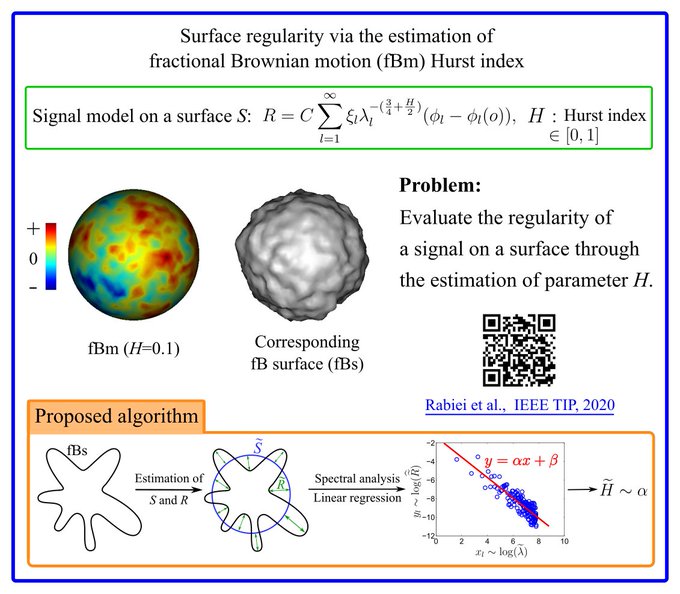
The recent definition of fractional Brownian motions on surfaces has raised the statistical issue of estimating the Hurst index characterizing these models. To deal with this open issue, we propose a method which is based on a spectral representation of surfaces built upon their Laplace-Beltrami operator. This method includes a first step where the surface supporting the motion is recovered using a mean curvature flow, and a second one where the Hurst index is estimated by linear regression on the motion spectrum. The method is evaluated on synthetic surfaces. The interest of the method is further illustrated on some fetal cortical surfaces extracted from magnetic resonance images as a means to quantify the brain complexity during the gestational age.